A tool for autonomous and performant benchmarking of facial expression analysers

What’s that? In mathematics and computing, these are well-known problems that address real-world issues by calculating maxima or minima of a series of parameters in order to optimise a specific function called objective function. Optimising allows one, for example, to find the shortest route between several points, or maximising the revenue out of a set of transactions. In simple problems where either the function, the parameters or all of these are linear or fixed, this is somewhat easy. But in most of real-world problems, such as the one of facial alignment, these are non linear, and their complexity skyrockets.

In order for AI agents, robots or software, to be able to understand the humans with whom they interact, solving this nonlinear programming is therefore necessary, as a more performant face alignment will mean smoother interaction. A team from INRIA, one of SPRING project’s partners, has made a significant leap towards that objective.

Face alignment is the problem of facial landmark detection and localisation from a single (two-dimensional) picture. It provides input to a variety of computer vision tasks, such as head-pose estimation and tracking, face recognition, facial expression understanding, visual speech recognition, etc. [2, 3]. Two dimensional face alignment is already well mastered, and the most recent methods making use of deep neural networks show excellent performance, at the notable exception of occlusions [4]. Indeed, two-dimensional methods cannot account for points absent from the image, such as when a face is turned sideways, or partially hidden behind an object, such as shown below.

Six samples from the AFLW2000-3D data set [5] that was used for this study showing partial occlusions of various sorts.

In such cases, three dimensional face alignment (3DFA) algorithms become necessary. Although plenty of 3DFA solutions exist, there was until now no automated and robust way of benchmarking their performance. Traditionally, performance analysis relies on carefully annotated datasets (that is, mappings of the 3D coordinates of a set of pre-defined facial landmarks). However, this annotation process, be it manual or automatic, is rarely error-free, which negatively influences the result of the analysis.

In contrast, the INRIA team proposes a novel, fully unsupervised methodology based on robust statistics and a parametric confidence test, bypassing annotations. Put simply, this method takes advantage of the fact that faces can only undergo rigid transformations. For example, change in scale  in the case of facial expressions, rotation or translations for movement and occlusion; augmented with picture noise to account for image granularity and lighting conditions. By providing a statistical estimation of these transformations (by reference to a frontal facial picture), this method allows one to map an unknown face onto a model face, thus allowing to measure face-to-model discrepancies.

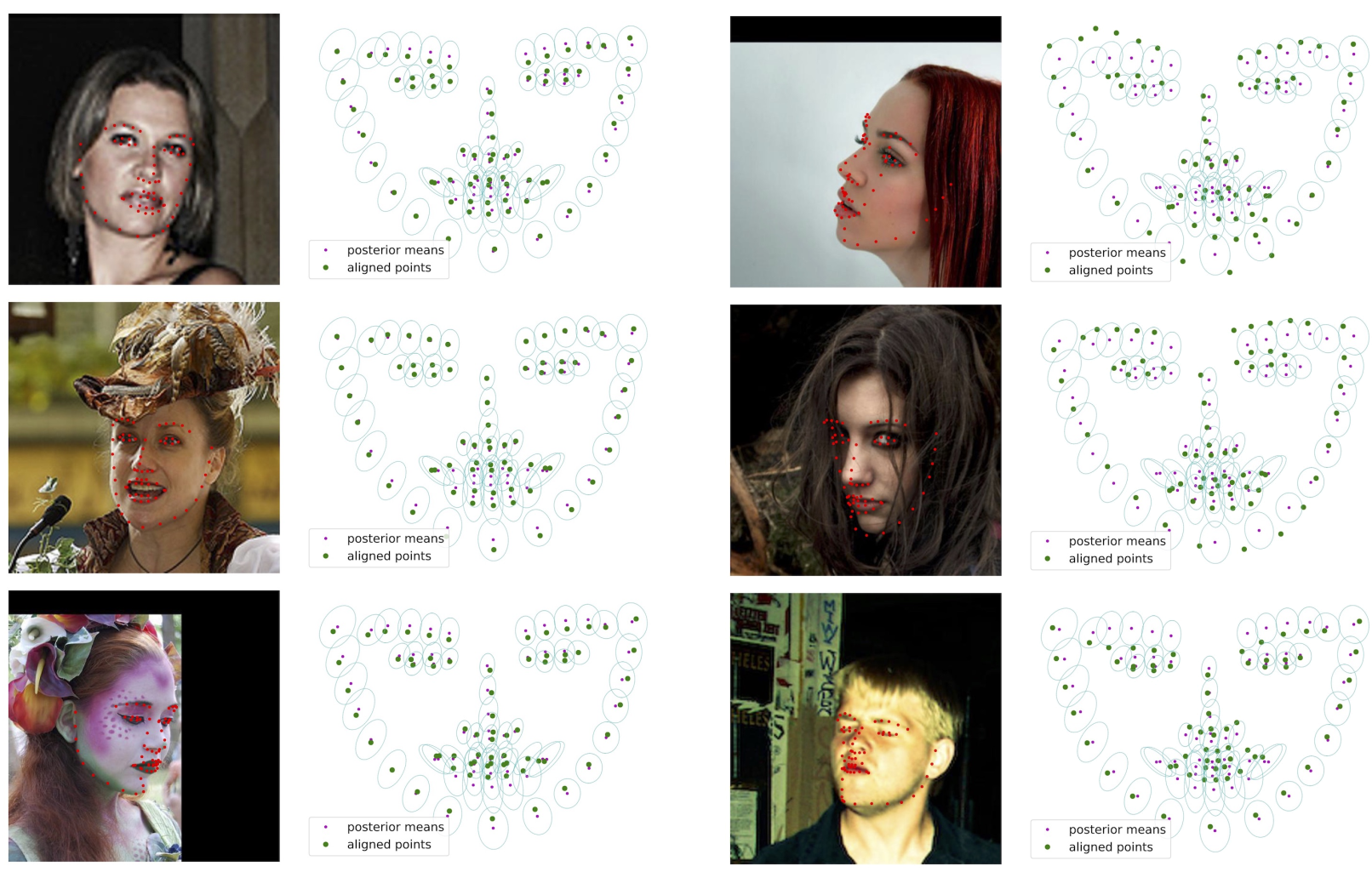
Face landmarks extraction with an in-house 3DFA algorithm called GStudent-EM. Left panel, examples of good scores; right panel, example of worse scores.

In detail, this method is based on the so-called heavy tail probability distributions. Imagine two groups playing darts: one of experts, one of beginners. Both are requested to hit the centre of the dartboard. In the expert group, it is highly probable that a large amount of hits lie in a small area close to the centre. However, in the beginner group, you will have a much more spread and biased hit distribution and it is now highly probable to get hits very far away from the centre: this is a heavy tail distribution. The exact same happens with annotations of facial landmarks. By acknowledging this fact and building appropriate models of heavy tail distributions, the Inria team was able to make their 3DFA algorithm and assessment method more robust to these spread and biases.

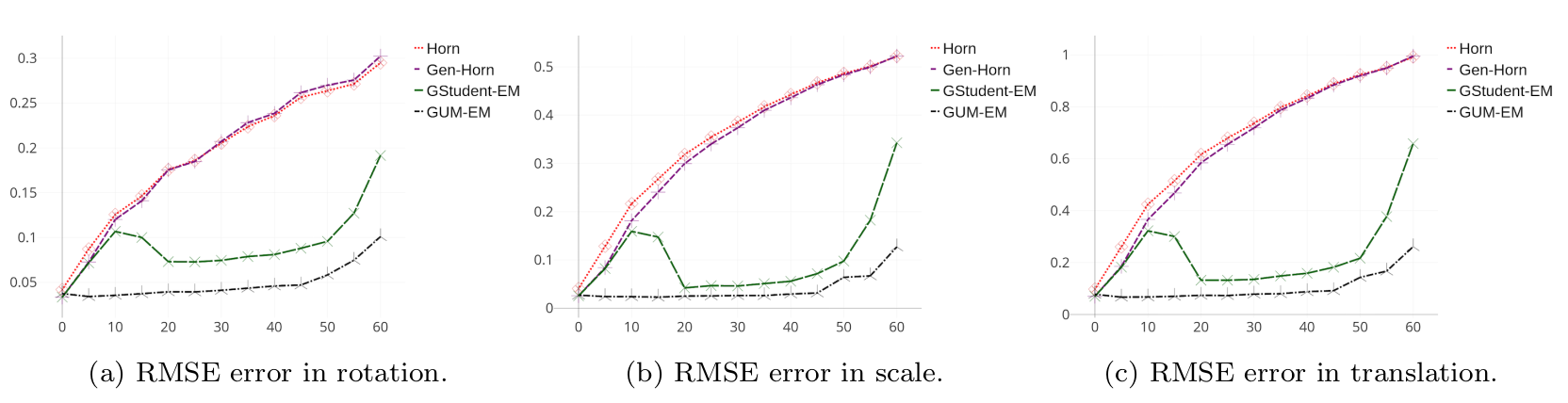
Root mean square error (RMSE error) between the estimated landmarks and the observed ones, as a function of the percentage of occlusions in three different cases: rotation, scale, translation. The error stays relatively small up to 50% occlusion in the case of the two algorithms tested in this study, GUM-EM and GStudent-EM, while two classic methods derived from Gaussian distribution show a constant increase of the RMSE error [6].

The result of this study is a fully unsupervised analysis method, robust to up to 50% occlusion and/or noise, which makes it suitable for mapping a face, from an unknown pose to a frontal pose, even in the presence of facial expressions and occlusions. The method being neither method-biased nor data-biased, it can be used to assess both the performance of 3DFA algorithms and the accuracy of annotations of face datasets.